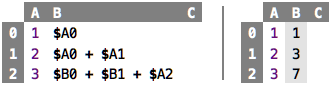Chapter 1: Values and Expressions

Primitive Values

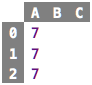
Numbers such as 7 or 42 are values. A value, as its colloquial meaning implies, never changes. A 7 will always be a 7, it won’t spontaneously become an 8. An 8 is a different value. In the following spreadsheet, all the 7s are indistinguishable: the value appears in three cells, but none of them is different than any other one. They are exchangeable. Consider money: even though the various 10 EUR bills are different “objects” (indentified by their unique serial numbers), to you, they are all the same. 10 EUR are 10 EUR.

src

There are other kinds of values, too. For example, "Hello" is a string value, i.e., one that represents a text, and not a number. Again, all "Hello"s are the same, there is no reason to prefer one value "Hello" over another value "Hello". A third important class of values are truth values, also known as Booleans, after George Boole, who contributed to mathematical logic. There are only two values in this category, true and false.

Numbers, strings and Booleans are the kinds of values we will work with for now. They are available in all programming languages (sometimes with other names), and most other, more complex values will be composed from those.

The value "42" is also a string value, it represents the text that consists of the two digits 4 and 2. It doesn’t matter that the text could also be interpreted as a number; as long as it is enclosed in quotation marks, it is a string. Later in this tutorial we will learn how (and why) we would convert the text "42" into the number 42.

Computed Values and Expressions

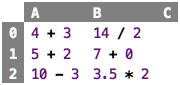
Values can be computed. In the sheet below, all cells, when their value is computed, will contain the value 7.

src

We call something like 3 + 7 or 14 / 2 an expression. When an expression is evaluated, a value results. This is maybe the most important sentence in this whole tutorial: Evaluating an expression results in a value. The word “evaluation” literally means to “produce a value”. We will see that a whole class of useful programs can be written using (increasingly more complicated) expressions.

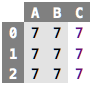
The display of sheets can be changed to show the results of evaluating the expressions in the cells; see the sheet below. The first two columns are the evaluated versions of the first two columns of the previous sheet.

Explain how to switch notation

src

The third column contains three primitive values 7 . If a cell contains a primitive value (such as 7), then the result of the evaluation is the value itself – evaluating a primitive value, or literal, results in itself. Note how, in the spreadsheet computed values, when shown in their evaluated form, use a grey background to indicate that you cannot change that value directly, because it is computed; instead, you have to change the underlying expression.

You can press F2 to reveal that expression and then change it. You can see the background color change, and you can then modify the expression. Press F2 again to show the value.

You can evaluate an expression any number of times, the result will always be the same. You could argue that each evaluation computes a different, new value, but since we have seen above that all values with the same denomination are identical, this observation is meaningless. Thus, when you see an expression, you can always evaluate it to get a value. If, for whatever reason, you evaluate it several times, this does not matter, you will just always get the same resulting value. Conversely, if you know an expression didn’t change, you can store the resulting value when it is evaluated first, and, when asked to evaluate again, you can return the previously computed value.

The process of storing values once they have been computed and then returning that stored value when asked (typically several times) is called caching. Caching generally makes systems faster, but it also requires more memory to store all those previously computed values. This is the kind of trade-off programmers have to make all the time. However, note how this trade-off concerns the engine that runs the programs you write; as a person who writes programs, i.e., as the reader of this tutorial, you don’t care exactly because from the perspective of what the program does, it doesn’t matter – the semantics of what it means to evaluate an expression does not change.

Basic Operators

We all know the basic arithmetic operators from school: +, -, * and /. The last one, division, requires a little bit more discussion later, because it is not obvious what should happen if we divide something that does not result in an integer number (such as 7 / 2): should the result be a real number (3.5), or do we expect to get an integer and the remainder (3 remainder 1). Also, the special case of division-by-zero, which, we remember, is illegal, has to be dealt with. But we ignore all of these details for now.

The first row in the sheet below shows a few arithmetic operators, and their results (in the sheet on the right). As you can see (and certainly remember from school), you can chain arithmetic operators, according to their precedence (* has higher precedence than +, for example).

src

From school we also know the comparison operators: > greater, >= greater or equal, < less, <= less or equal, == equal and != not equal (in school you probably used = for equality; in computing, the double == is common, so we stick to this convention). These operators are defined on numbers, and in contrast to arithmetic operators, they cannot be chained; which is why the second row of the table above shows only pairs of numbers with an operator in between. They evaluate to a Boolean value, i.e., they “say yes or no” to your question whether one number is bigger/smaller/equal etc. to another one. The arithmetic and comparison operators can of course be combined, so you can write 3 + 5 > 7 * 2, and this evaluates to false. For this to make sense, the arithmetic operators must have higher precedende than the comparison operators (the expression above must mean 8 > 14 and not 3 + false * 2; that would make no sense.

“Makes no sense” is handwaving for a type mismatch: you can only perform arithmetic operations on numbers, and false is not a number. We will return to types in Chapter 3.

While there might be many more operators in any particular language, I want to close this discussion with one example of the conditional operator if; examples are shown in the third row of the spreadsheet above. In contrast to all the other ones, it takes three arguments, not two. The first one must be a Boolean value; if it evaluates true, the overall if evaluates to the expression given in the then part; otherwise it evaluates to the one given in the else part. Again, this one binds even less tightly than the comparison operators, so you can write complex expressions like the one given in the C2 cell. We will return to more sophisticated means of making (conditional) decisions in will return to types in Chapter 7.

References and Dependencies

Let us go back to spreadsheets and take a look at the following one:

src

On the left we see the expressions in the cells, on the right we see the values that result from evaluating the expressions. Like in Excel, we use the $ notation to refer to another cell by its coordinates. More specifically, we retrieve the value that is evaluated from the expressions in the cell identified by the coordinates so we can use it to calculate the value for the current cell. So, when we evaluate cell B0, then the evaluator sees the $A0 reference which prompts it to retrieve the expression in cell A0 and evaluate it, resulting in 1. Since B0 has no further content, this 1 becomes the value of B0. Similarly for the B1 cell: it gets the value of two referenced cells, and then adds those two values, producing 3 as the value of B1. And so on with B2.

This is a good place to introduce the notion of a dependency: a cell X that contains a reference to another cell Y is said to depend on Y. You cannot compute the value of cell X without first having calculated the value for cell Y. Dependencies are widespread in programming, and they are often undesired because they “chain” parts of program together. We will learn several ways of avoiding such dependencies as we progress through this tutorial.

Evaluation Order

One thing dependencies do is to enforce an order in the evaluation of expressions (or cells, in our example here). So, looking at cell B2 in the sheet above, the dependencies are as follows (the arrow should be read as “depends on”):

B2 -> B0
      -> A0
   -> B1
      -> A0
      -> A1
   -> A2   

Thus, since we have to evaluate the cells in the opposite order of their dependency, a possible evaluation order is

A0, B0, A0, A1, B1, A2, B2

Notice how in the evaluation of this cell we evaluate A0 twice! We know that evaluating the same expression multiple times results in the same value. So this allows us to remember (cache) the value calculated during the first evaluation and return it, without any new computation, when we evaluate A0 for the second time. If the computation of A0 is expensive (i.e., requires lots of computational work itself), avoiding multiple recomputations can make a significant difference in performance. And yes, in the intro I told you that I don’t want to teach you performance optimization, but I think it is still useful to get some glimpse into how programmers go about making software fast.

So, let us think about how we would evaluate the whole spreadsheet. The first alternative is to linearly step through all cells and evaluate each in turn. This means that, by the time we arrive at B2, all other cells will already have a value, and we can use those previously computed values to perform the computation in B2. In the end, this means that our dependencies effectively become

B2 -> B0 [cached]
   -> B1 [cached]
   -> A2 [cached]

Because of caching, we can ensure that each cell is only ever computed once, no matter how often it is referenced from other cells.

What happens if the user changes the value of A1 from its current value 2 to, say, 42? A naive strategy would reevaluate the whole spreadsheet: whenever any value in any cell changes, we reevaluate everything. However, there is a better strategy: because we know all the dependencies of all the cells, we can only reevaluate those that depend (directly or indirectly) on the one the user changed. So, based on our dependency graph above, changing A1 will result in the reevaluation of B1 and B0 only (and, of course, of A1 itself). This is obviously a much cheaper operation than reevaluating everything, and the ratio becomes more favourable the bigger the spreadsheet gets.

So, what do we learn? Understanding the dependencies in a program allows us to be clever about how we execute the program. This is true not just in spreadsheets, but it is especially easy to spot there. It is a lesson you will see all over programming.

What does it mean to execute a program?

This is a good time to ask what it means to execute, or “run”, a spreadsheet-style program: it simply means updating the values of all cells. As we have seen above, there are several (more or less clever) strategies for doing this, but updating the cell values is all there is. In addition, all the data the program works with is readily visible in the spreadsheet, it is simply the content of all cells. This very simple execution mechanism and the transparency regarding a program’s internal data (it’s all in the cells!) makes spreadsheets so attractive and explains their widespread use (together with their nice formatting options).

However, as we will see, spreadsheets are just one member of a whole family of programming languages called “functional”, for which the same properties hold regarding the execution model and the the transparency regarding internal data. We will elaborate on this in detail as we proceed with this tutorial.

What are Cells?

In spreadsheets, cells play a central role: a spreadsheet is simply a collection of cells. A cell contains “code”, i.e., an expression, and when evaluated, it represents a value. A cell, thus, identifies a value: you identify it via its coordinates (e.g., A0, B2, etc.). The value of a cell only changes as a consequence of a user’s edits: either the user changes a cell content directly (which triggers its own reevaluation), or the cell is reevaluated because it depends on a cell that changed (for any of the two reasons given here).

One way of looking at this is that, whenever the user changes the contents of any cell, the functional (spreadsheet) program is reexecuted, updating all other cells. Another way of phrasing it is to say that a functional program never really runs; the program is the computation.

If you have had some exposure to programming before, you have probably heard the word “variable”. Are cells variables? Not really. Similarly to cells, a variable is a name for a value. But more specifically, and more technically, it refers to a location in the memory of a computer. What is stored inside that location can change during the execution of a program. So, for example, during the first half of a program’s execution, the value of a particular variable might be 0, and during the second half of the execution it might be 1. Programs that use variables can contain statements that update the values of variables. A spreadsheet, and more generally, a functional program, cannot do this. Once a value is assigned to a cell during a particular program execution, it will never change (this realization is what allowed us to cache the values in cells in our earlier discussion on execution strategies). There is no “update cell value” command in spreadsheets.

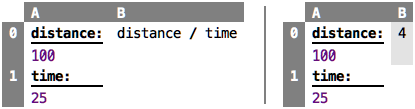
Naming Cells and Values

To recap: a cell is simply a way of identifying (potentially computed) values in a program. By default, you identify a cell through its coordinates (B4). However, you can of course also give cells specific names (again, the evaluated version is shown on the right):

src

This is still a regular spreadsheet, except that we now assigned names to cells A0 and A1, and we use these names in the expression in cell B0. Names are really important to make a program understandable: the above example is immediately and intuitively understandable. Make sure you spend some brain cycles on good names!

Instead of naming cells, we can also extract this same information into val declarations. You can imagine those simply as “cells outside a spreadsheet”: their value is still calculated only once (per program execution).

src

Finally, we can get rid of the spreadsheet completely:

src

Notice that we did not change any of the semantics of the program (semantics refers to what a program means, i.e., what happens when it is executed). These are still three values, all are executed only once per program execution, and the dependencies …

speed -> distance
      -> time

… determines the order in which they are executed. Congratulations, you have just made your first step outside of spreadsheets, you wrote a simple functional program.

Continue with Testing Programs

ProgrammingBasics

How to think like a programmer.