Go back to Values and Expressions
Chapter 2: Testing
Testing is usually not discussed this early in tutorials like this. However, I want to make it a habit in you to always test the code you write. And I will also use tests to demonstrate what code does in the remainder of this tutorial. This is why we introduce it early. Enjoy :-)
Trying out Programs
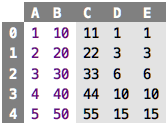
So far, we have assessed the correctness of a program by “looking” at it. For example, consider the following sheet, which is intentionally a little bit more complicated than the ones we saw so far:
The first two columns are just values. The third column sums up the first
and the second. It uses an alternative way of referencing cells: instead
of using their absolute coordinates, we use relative navigation. l
goes one cell to the left, ll goes two to the left, and so on (there are similar
“moves” for right, up and ddown). Columns D and E are both
supposed to sum up the values in A up to whatever row we are in; they
use different ways of calculating that sum. Here are the values that
these cells calculate; are those correct?
Ultimately you have to perform the calculation manually and compare what
you get there with what the program computes. For example, for column
C, you might intuit that the values are correct because the two digits
of the sum are the same: if you add X and 10 * X, you get a
repdigit XX (at least if X is smaller than 10). For the D and E cells it is not quite so simple. But here
we can observe that we perform the same computation twice in different ways, once
explicitly (using the sums of $-references) and once using a slightly
more sophisticated expression which we don’t have to understand in
detail for now. And since the values in D and E are the same, it’s
maybe relatively likely that they are correct.
Do the same thing twice …
So this is the first thing we can note about testing: essentially, you do the same thing twice using different approaches and then check that the two produce the same result. One of these two approaches might not involve a computer; you perform the calculation in your head, or somebody tells you what they expect the result to be. If the two agree, this means that your program is correct … or that they are both consistently wrong! How can you ensure that it is the former and not the latter?
Ultimately, we cannot really be sure, but we can use the following strategy to dramatically improve the odds: we can make one approach much simpler than the other. The (potentially) complicated one, usually the one calculated by the program we want to test, is called the actual value The simpler one is called the expected value. Ideally, the way we come up with the expected value is “obvious”, i.e., it is so simple that nothing can go wrong.
… compare explicitly …
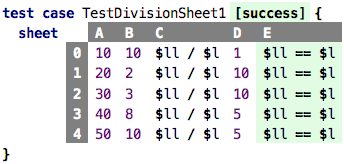
Once you have a way of determining the expected value, you write another part of the program, called a test case, in which you explicitly compare the actual and expected values. Each such comparison is called an assertion:
Why is there no space between the assert and the $
You can run a test case like any other program: it evaluates the
actual and expected expressions and then compares the two. If they
agree, the assertion succeeds, otherwise it fails, as shown by the green
and red background color; it also shows the actual value if the two
disagree. A test case succeeds if all assertions in the test case
succeed.
Test cases can be evaluated by either pressing
Ctrl-Alt-Enter. You can use this key combination on a single assert, on a complete test case as well as on the overall test suite. In the latter two, all asserts under that particular node are executed.
Notice how, in the example test case above we use cell references that are qualified with the name of the sheet to peek into that sheet to access cell contents.
There is a neat trick in the context of spreadsheets here: you can use a whole sheet inside a test case:
If you do this, all cells with Boolean values are implicitly interpreted
as an assertion: if the value is true, the assertion succeeds otherwise
it is interpreted as a failure.
… and then automate
You test for two reasons. First, you want to ensure that a program is
correct at the time of writing it. Here you could argue that just
“looking at” the execution of a program and manually inspecting actual
values is good enough. However, the second reason for writing tests is
that you want to make sure your program remains correct over time, as
you are required to make changes to your program. For example, somebody
might change how the makeList thingy works, breaking your spreadsheet.
How do you find this problem?
As we said above, you make the tests a part of the program. Essentially, one part of your program (the tests) “looks at” that part of the program you want to test (the tests subject). So far so good. But then you also have to make sure that you automatically re-execute the tests whenever you make changes to your program, or at the very least, before you use your program in the real world, to do real stuff. This is why test automation is crucial: you write tests, you ensure that they are green when you write them, and then automated tools called integration servers, run them all the time. They notify you if something breaks. You can then run the test locally, investigate the problem, and fix it.
The problem of coverage
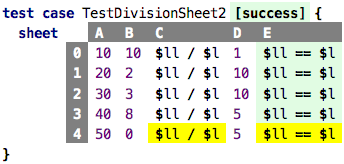
Let us look at the following sheet (which is used in a test case, which is why the Boolean cells are colored green/red depending on whether the condition is true or false):
All our divisions in column C work correctly, so everything is fine,
right? Of course
if only we had thought of testing the division by 0, then we would have
noticed that our program fails in this case; the cell becomes yellow to mark
the internal error.
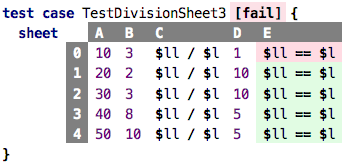
Or if we had tried to divide 10 / 3 we would have noticed a problem with the number of decimal digits in the result:
So what does this tell us? Testing has a coverage problem. We have to test all relevant cases to build complete trust in our program. It is not always easy to ensure this: we might simply forget to test a corner case, or there might be something particular about how the to-be-tested program is written that makes it fail for particular inputs. How could we know? We can’t. Testing is by necessity an imperfect science. But this does not mean we shouldn’t do it: some assurance of correctness is better than no assurance at all.
Of course, computer science has ways of dealing with this problem. For example, we can measure the actual coverage, and continue to write tests until the coverage is 100%. We can also rely on test case generation, which, through fancy algorithms, automatically generates tests to make coverage 100%. Finally, we can use formal verification techniques that analyze programs for correctness (as opposed to systematically trying them out through tests). However, all of these techniques are beyond the scope of this tutorial. And except for coverage measurement, these techniques are actually not used that much, even by professional programmers.
Is my expected value correct?
Let’s say somebody tells you to write a program. If you will, he is your
customer, and you “sell” them a program that performs the kind of
calculations they are interested in. You talk to them, and you understand
that they want a spreadsheet that in column C sums up columns A and
B. You build the sheet, and being a careful person, you also write
tests that successfully ensure the correct summation of the values in
the two columns. All is good. Except: your customer actually wanted you
to build a sheet that computes the difference between columns A and
B: you misunderstood the requirements. So there was a problem even
though your tests were all green. What can you do about that?
One way of catching this issue is to let your customer review the tests. If they are written in a sufficiently “customer-friendly” way, this is completely feasible. Your customer will see that the tests are all green, but they will likely notice that the tests are wrong relative to what he wants the program to do. Problem solved.
A second way of ensuring that the tests (and thus implicitly, the program) are valid and not just technically correct is to ensure that (some of) the tests are written by somebody else, somebody who also talks to the customer and independently builds an understanding of what the program should do. This makes it less likely that there is the same misunderstanding between the customer and this second person. Notice how we again “do the same thing twice”, but that thing is now the understanding of the customer requirements. This is of course more effort and involves more people – but hey, quality has a price!
Where does this leave us?
As we progress through this tutorial, we will make it a point to write tests for most of our examples. This is why we introduced testing this early in the tutorial. Writing tests along with your code is good ractice, and you should make it a habit: untested code is essentially useless code.
Continue with Types