Chapter 03: Types

What are types

At the beginning of the first chapter we talked about different kinds of values. We mentioned numeric values (7, 10 + 2, 33.33), string values ("Hello") and Boolean values (true and false). We should have said “type” instead of “kind”, because these are the most fundamental, or primitive, types available in essentially all languages: number, string and boolean.

A type represents a set of values. Again, as we said before, the boolean type represents the set that contains the values true and false, the type number represents the (infinite) set of numbers from -inf over -1, 0, 1 to +inf and string is the set of all possible texts, including the empty text "". When we have a value in hand, we say that it “has a” type or “is of” type.

Types as an analysis result

So what can we use types for? Consider this example:

src

This program does not explicitly say anything about types; no type is mentioned anywhere. However, we can query every expression for its type. If we do this on the 100 expression, the type will be reported as number[100|100], i.e., the type of numbers between 100 and 100. The range is only one element because of course we know the specific number, so the type can be very precise. We can also ask for the type of the whole val; that type is also number[100|100]. Why is this? Because by default, the type of a val is inferred to be the type of the value’s expression. The type for time is then number[20|20], not a big surprise.

You press Ctrl-Shift-T on a program node to query the IDE for the type of that node.

Let us add some more code:

src

The type of twoDistances is more interesting. Its type is number[200|200], so the types are automatically computed to reflect ranges based on the arithmetic operator *. For maybeDistances it is even more interesting, because, depending on whether someBoolean is true or not, the resulting value is either 100 or 200; so the type of the if is number[100|200] to make sure it can represent both outcomes.

Actually, we could be more precise: the type is either number[100|100] or number[200|200], because no value other than 100 or 200 is possible. However, in this particular language, a number type can have only one value range. This means that number[100|200] is the best way of approximating that the value is either 100 or 200. The type systems of other programming languages could potentially be more precise here.

Finally, what is the type of speed? It is reported to be number[5.0000|5.000]{inf}. That looks strange, it is the type of all numbers between 5.000 and 5.000, with an infinite number of decimal points. The reason is in this language, a division always leads to a type with infinite precision (i.e., a real number).

Before we move on, we should probably define the term type system: it refers to the set of rules that govern type correctness of a program. For example, the fact that any division results in an infinite-precision number is a rule that is part of the type system of this particular language. Similarly, the fact that numbers “adjust” their ranges according to the operator used, is part of the type system. The type system is also responsible for reporting errors if users do things that are not allowed by these rules, for example, trying to add a number and a Boolean (we will cover this in the next paragraph). The type system is also responsible for inferring types, which means that the type of a program node is computed from the type of one or more other program nodes automatically. For example, the type of the val is inferred from the type of the expression on the right side of the = in the val.

In the example so far, we have only used type inference: our program never explicitly mentioned anything about types, but the underlying analyser has computed types for us, and we can use those types to help us understand the program. Let’s move on now to explicitly mentioning types in programs.

Types as Constraints

Look at the following program:

src

Here, we have used the : notation to specify a type explicitly. More specifically, if we specify a type for a val, we express that whatever expression we use on the right side of the =, its type must be compatible with the one given explicitly. For example, we say that the distance must be a number between zero and 1,000 and it must have zero decimal digits (zero is the default, we didn’t specify it). For the time we specified a positive number with two decimal digits. The resulting speed is constrained to be a positive number with infinite digits (again, every division always gives infinite decimals in the result). How is this useful?

Well, if you tried to use a value greater than 1,000 for the distance, or a negative value for the time, you would get an error. Importantly, you would not get the error when the program runs; instead, you get the error already when you write the program. So the analyser that is part of your programming environment performs certain checks and reports them to you as early as possible.

Note that this is kinda similar to testing. In testing, we said that you specify the same thing twice, and then check one against the other. Here, too, you specify something twice: the set of allowed values (the type) as well as a particular value. If the set does not include that value, you get an error, In some sense, the programming environment tests the program for you, based on your specification of types.

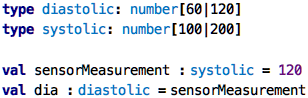
Take a look at the following example from a medical system, and you can see how types have the potential to avoid errors:

src

Explain better. Where is the error?

Type Compatibility

In the section above I said that “its type must be compatible” when referring to the expression used to initialize a value with an explicitly given type. So, if we have

val v : T = <expr-of-type-U>

then what does it mean for U to be compatible with T? Obviously, if T is the same as U, then the compatibility criterion is satisfied. So, if we wrote

val v: number[5|5] = 5

val s: string = "hello"

then everything is fine. But how about this?

val v: number[0|100] = 5

The type of the 5 is number[5|5], so is this compatible with number[0|100]? It is easy to see that it is if we go back to the notion of types as sets: if the set of values represented by U is a subset of (i.e., is contained in) the set of values represented by T, then U is compatible with T. We also say that U is a subtype of T. The notion of subtyping, or more generally, specialization, will become important later in this tutorial.

Wait, but …

… why do I need to specify the type for something if, as in vals, I also always have to give a value and that value can never change? Well, dear reader, you have a point here. Explicitly given types are much more useful if something can have several values as the program executes. In such a case explicitly given types are necessary to make the program meaningful. In the next chapter we will encounter a situation where this is the case: functions.

Continue with Functions

ProgrammingBasics