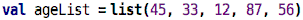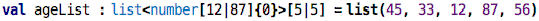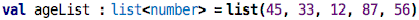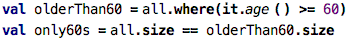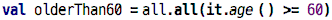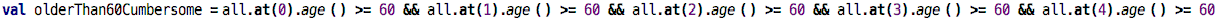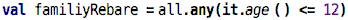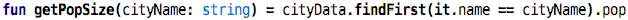View on GitHub

ProgrammingBasics

How to think like a programmer.

Go back to Structured Values

Chapter 06: Collections

Motivation

In the previous chapter we have discussed records. A record combines several values into a new abstraction. For example, values name: string, first: string and birthdate: Date are combined into a record Person. Collections are also abstractions that combine several values, but they are different from records in the following ways:

The reason for having collections is rather obvious: if we look at the PatientData example from the previous chapter, it’s rather strange to only have one blood pressure value. More realistically, you would probably want to collect several blood pressure measurements to represent how a person’s blood pressure evolves over time. Similarly, the introductory example from the last chapter …

  src

… can of course also be seen as a list of five records. We want to have an abstraction that allows us to work with collections such as lists, sets or maps.

Introduction to Lists

To get started, let us define a list of 5 integers:

  src

We define a value, as usual, but that value represents a whole list of other values, in this case, the ages from column A of the spreadsheet above. What is the type of this thing? Let’s see what the type system automatically infers:

  src

Wow, that is a rather complex type! Let’s see. It is a list. Inside the <...> it specifies the type of the elements of that list. In this case, all elements are (integer) numbers, and as we can see by analyzing the values, the number is between 12 and 87, the smallest and the largest of the values in the list. In the square brackets behind the angle brackets, the minimum and maximum length of the list is defined. Since we derived the type from the list value that had exactly five elements, the length is also be derived to be exactly five. Let’s see what happens if we generalize the type:

  src

Here, we have manually specified the type (i.e., we have changed the program by editing it) to just be a list of numbers; no number range, and no list length. This is still a valid program in terms of types. Remember that earlier we said that for a val declaration, the type of the value (list(45, 33, 12, 87, 56)) must be the same or a subtype of the specified type (if one is specified). This is intuitively the case here: numbers between 12 and 87 are clearly a subtype of numbers in general, and a list with five elements is a subtype of a list with an arbitrary length.

The fact that a list<U> is a subtype of list<T> if U is a subtype of T is a feature called covariance. So, in our language here, lists are covariant. They don’t have to be, the language (and its type system) could have been defined differently; however, covariance for collections is rather widespread and also makes intuitive sence.

So in the code above, we see the word “list” twice. Behind the colon it is used as a type, similar to number or Person. What is special about this type is that it also specifies the type of the elements in the list between the angle brackets. This is new: one type (list) has a second type (number) as a parameter. We will return to this below. The second use of list is behind the equals sign. As we know from earlier examples, we expect an expression there. So the list(a, b, ...) is an expression that constructs a new list. The elements of the list are given in parentheses. If it is supposed to be an empty list, you can leave the list of elements empty. However, then you have to specify the type of the elements explictly (because the type system cannot derive it from the elements). Here is an empty list of strings:

  src

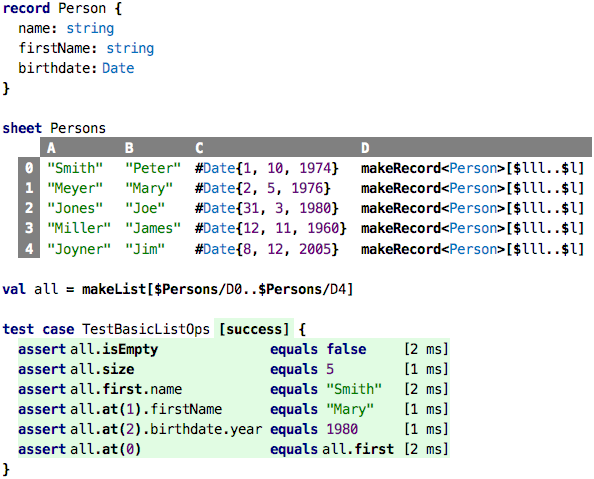
There are of course other ways of creating lists. Below we will see how to create new lists by adding or removing elements from an existing list. However, we can also construct completely new lists in other ways than with the list expression. Here is a way to construct a list from a linear range of cells in spreadsheet:

  src

Each row in the sheet, in row D, creates a Person value instance using the makeRecord we have seen before. We then declare a value all that is a list<Person>; it uses makeList to grab the persons in column D of the spreadsheet. The tests also demonstrate how we can process lists; we will discuss this next.

Processing Lists

Let’s look at what we can do with lists. The tests in the code above demonstrate the basics. Fundamentally, everything we do with lists, once they are constructed, uses dot notation. First we check that the list is not empty; isEmpty returns a boolean. Then we ask the list for its size and expect 5. We then use the first operation to get the first Person in the list; we chain a .name to retrieve that person’s name and assert that it is “Smith”. Using at(pos) we can retrieve the element at position pos. Note that these positions are 0-based, like all indices in computing. The last assertions demonstrates this.

The fact that positional indices use 0 for the first element can only be understood historically. In the early days, lists were stored simply as successive entries in the computer’s memory. So, for example, the list 45, 33, 12 was stored, in binary encoding, one byte each, directly next to each other: 00101101|00100001|00001100. Since we know that each number takes one byte (8 bits, count the digits!) for storage, we can access the n-th list entry by adding n bytes to the address of the beginning of the list. So assuming the list was stored at address ABE0 (a hexadecimal address value), we can retrieve the n-th entry from address ABE0 + n. This is a very efficient way of retrieving data, because it requires no iteration. Anyway, it is clear from this discussion, that the first element of the list is right at the beginning of that memory block, so we have to add 0 to the base address. This is why we use zero-based position indices. Today, of course, in many languages data is stored differently, and the fact that we use a zero-based index is pure convection. But we stick to it :-)

The next set of examples introduce something fundamentally new: we will use expressions as arguments to function calls! So far, we have only ever passed values to functions, i.e., data. Now we are passing code to functions. Functions to which we can pass code are called higher order functions. This is a somewhat advanced concept if you try to understand how it works under the hood. I will explain this later in the tutorial, Chapter 8. For now, we will just use these new kinds of functions, and using them is actually quite easy and intuitive.

Mapping: Let’s say we want to create a new list from the existing example list above that contains only the name of each person. So we will step through the all list, access the Person at each index, grab their name, and then package all of these into a new list. Here is how you do this:

  src

The value onlyNames is now a new list (all of course remains unchanged) that contains only the names. As the first assertion shows, the two lists have the same size, not surprisingly.

So how does map work? The map higher-order function internally runs through all the elements of the list on which we call it (here: all). For each element, it calls the code that we pass to map. That code is an expression, that creates a new value. These new values will be packaged into a new list, which is then the value returned by map. The code we pass, can use the special expression ìt to refer to the element from the original list for which we’re currently calculating the new value. So because we map over a list of Persons, it is always of type Person. This is why we can call .name on it. The resulting list is now a list<string>. So to be clear: the it.name is called five times in our example, once for each of the five persons in the all list. The iteration, and the calling, is handled internally to map.

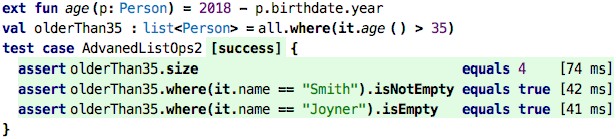
Filtering: We can also filter the contents of a list according to a criterion. Look at this code:

  src

We first define a function age that computes a person’s age based on their birthdate and the current year. We then take the all list and pick from it only those elements where the age is older than 35 (remember that we have defined age as an extension function, so we can use it in dot notation). Like the map function, where does this by calling the expression we pass to it for each element in the list. But instead of creating a new list with the result of that expression, it uses the element from the old list, but only if the expression we pass as an argument evaluates to true. So the resulting list is still a list<Person>, but it might have fewer elements than the original, because those where the expression is false are not included. In our example, only the last element in the list, Jim Joyner, is younger than 35. The two last asserts in the tests illustrate this.

Checking: Lets say we want to buy a train group ticket for the folks in the all list. We can get the retired rebate if all of the people in the group are older than 60. How can we check for this? One way is to use where: we write essentially the same code as before, but use 60 as the age threshold. Then we check if the filtered list has the same length as the original one:

  src

There’s a simpler way though, and it looks like this:

  src

The all operation also takes a Boolean expression. And it evaluates to true if the expression is true for all elements of the list. Otherwise it returns false. In terms of Boolean algebra, it joins all of the expression by and. You can see how this is cumbersome if you wrote it manually:

  src

There is also the correponding function for or-ing the elements together. Let’s say we get the family group rebate as soon as there is one group member under 12 years of age:

  src

For the math-minded people among you, all is the universal quantifier (represented with the upside-down capital A) and any is the existential quantifier (represented with the left/right-mirrored capital E).

There are many more (higher-order) functions on lists that do all kinds of fancy things. Some are not so easy to understand, and we will ignore those for now. What is important here is that you understand the idea of lists as ordered collections of similarly-typed elements, and that you get a feeling for this notion of “passing code into functions”, as a way of parametrizing the function with specific behavior.

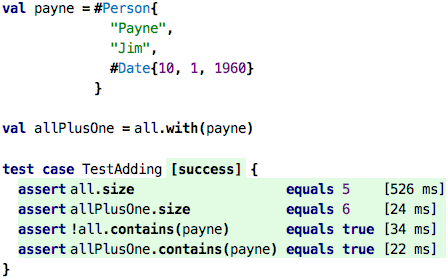
Adding and Removing Elements: We already used higher-order functions to create a new list from an existing one, but we only did it as “bulk” higher-order functions. How do we add a single new element to a list? Here is how:

  src

Using the with operation, we can create a new list that has the contents of the original one as well as the one passed as the argument of with. Because lists are values, the original list remains unchanged, as the test shows. So, above, we should not have said “how do we add a new element to a list”, but rather, “how can we create a new list from an existing one that has one more element in it”.

Databases and the System Boundary

Based on the observation above that we can not change any particular list, but only create new ones with additional elements (or fewer, using without), how would we build a database? A database is a store of records where programs can add or remove records as the program executes. The database, i.e., the list of values, changes over time. If this is the case, a database, by definition, is not a value, because it is not immutable. At different times during the execution of a program a particular database has different contents. The database is a variable.

In this part of the turorial we do not (yet) look at language features that support to change over time because it makes writing, understanding, and debugging programs much more complicated. It is beyond (at least a strict definition of) functional programming. So variables, and thus, databases, are out of the picture for now. So how can we use the skills we have obtained so far for something useful? How can we write a useful program if we cannot keep track of how stuff changes over time? Take a look at the following picture:

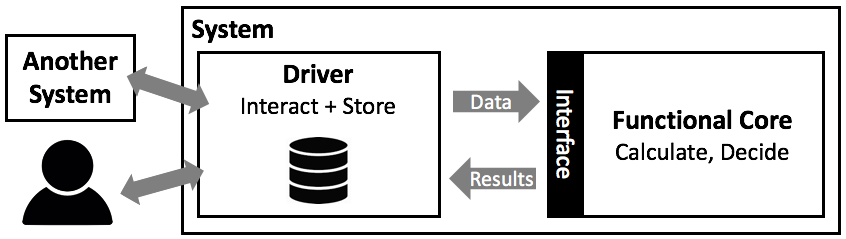
Let us say we are responsible for building a tax calculation system: based on input from all kinds of other systems and interactions with users, the system is reponsible for calculating the different components of the tax a citizen has to pay each year. As software architects, we use a principle called separation of concerns (we will discuss this and a few others later in this tutorial), where we try to isolate different aspects of the overall problem. In this particular example, we distinguish between two aspects: the core of the system that performs the actual calculations and decisions about what and how much somebody has to pay for a given time period based on data that is handed in, and a driver which interacts with the user, other systems and its own database.

The driver is in charge of “running the show”. For example, whenever a new month is over, the driver revisits all citizen under its purview, collects the data necessary for tax calculation from other systems, and then asks the calculation core to perform the actual calculation. Once that calculation is done, the core hands the results back to the driver, who then stores the data in a database and potentially triggers other, downstream systems.

Here is the thing: in this architecture, it is completely feasible to implememt the core as a functional program. So let’s say you are an expert in tax calculation, and your organization decides to use a DSL to represent the core calculations. If the system is built according to the architecture shown above, you can absolutely stay in the simpler, functional world. All the complexity of handling values that change over time is “outsourced” into the generic driver part, which is written by software engineers. Many systems are in fact built exactly this way. We will use this example later in this tutorial to illustrate many advanced ideas.

Here is how one could design the language part of such as system:

  src

In the left column you see a couple of records that represent the data that is used in the tax calculation. The driver is reponsible for populating these records correctly by retrieving data from its database or by interacting with other systems. As the tax expert we mentioned before, we don’t really care how the driver does this. In the right column you primarily see function that is used as the interface between the driver and the calculation core: the function calculate takes the data that is assembled by the driver (here: an instance of TaxCitizen) as well as the month for which we are supposed to calculate the tax. The function then returns an instance of MonthlyTax that it calculated based on all the complicated decisions and calculations that are specified by the tax law for the particular period. Calculating this correctly is the only thing this function (and hence you, the tax expert) is reponsible for. Once returned, it is the driver’s reponsibility to store the new MonthlyTax in the database and initiate downstream processes (such as printing a tax bill).

Sets

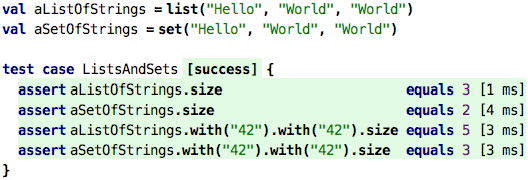
Like a list, a set also contains several values of the same type, and it specifies that type (and optionally, a size) as part of its type definition. So a set of strings would be a set<string>. However, sets are different in two important ways. First, its contents are not ordered. So asking for first, last or at(pos) does not make sense. The second difference is that every value can only be in the set once. Consider these tests:

  src

In the value definitions, in case of the set, the second World is not added, because there is already a value World in the set. This is why the resulting set only has two elements instead of three (the list has three). The same is true when adding the string "42" (yes it is a string, not a number, because of the quotation marks).

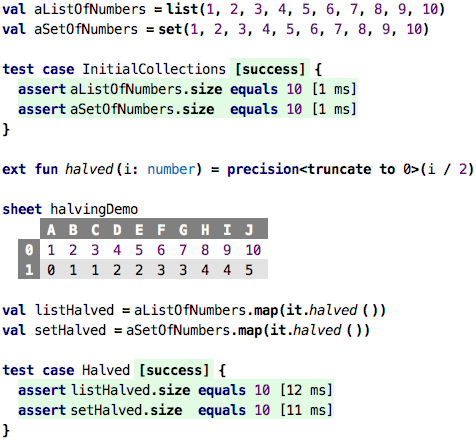
Consider the following example:

  src

We create a list and a set of unique numbers. No duplicates to be removed when creating the set, so both have a size of 10, as the test confirmes. We then define a function halved that divides a number by two, and then truncates is back to zero decimals. The sheet shows the results for the values 1 through 10. As you can see, this operation creates duplicates.

W now use map to apply halved to each of the elements of the list and the set (the higher order functions such as map, where, all or any are all available on sets as well). What will the result be? In particular, will a map (and similarly, a where) on a set produce another set and reduce the duplicates? According to the tests, it does not.

The reason is that all operations on any kind of collection (except lists), will give you a collection as a result. collection is the supertype of list and set. It is unordered (so you cannot use at or head) and it is also read-only (you cannot add using with). However, you can transform them:

  src

You can take any collection and transform it into a set using the toSet operation. Effectively, this is a way to remove duplicates. So if you do this with the listHalved or setHalved collections, you get a collection with 0, 1, 2, 3, 4, and 5. Its size is 6, and the first three elements are 0, 1 and 2, as the tests show. Of course you first have to transform the duplicate-free set back to a list to be able to access it by position.

Maps

Here is a sheet of the 10 biggest cities in Germany and their population in millions:

  src

How do you represent this as a data structure? One way would be to define a record CityData that stores the name and population size of a city …

  src

and then create a list of instances (using makeRecord) from the spreadsheet. Once we have this list, we can find the population for a city with the function shown next. This is the first time we use findFirst: it returns the first (and only the first) element in the list for which the condition passed as an argument (it.name == cityName) is true; the variable cityName inside the findFirst is a reference to the argument of the function.

  src

That’s reasonably ok, I guess. But we have to always scan through the list to find the CityData we are interested in, and then ask for its population size. The syntax is awkward, and from a performance perspective it also isn’t that good because we have to linearly scan through the list until we find something (that’s what findFirst does internally). Again, you shouldn’t be overly concerned with performance, but I thought it’d tell you :-)

In practice it is very common to associate one value (population size) with another one (city name), and all programming languages provide direct support for that using the map datatype (not to be confused with the map operation; even though, what the map operation does is also “associate” a new value with an existing one, by creatign that new collection).

  src

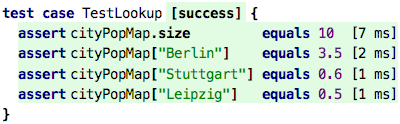
A map is a collection of key->value pairs, where all keys and all values are each of the same type (here: string and number). The respective type reflects this; here the type would be a map<string, number{1}>, a type with two type parameters (lists and sets have one). You can look up the value associated with a key using the bracket notation:

  src

Again, looking at performance, because of the way maps work internally, the lookup is very fast, independent of the size of the map. No linear scanning is required.

Here is how you add to maps:

  src

In the modifiedMap we have one more entry, the one for Heidenheim. The putting of Stuttgart overwrites the old value. This is because a map only stores one element per key. If you wanted to store several data items, for example, the population size and the state in which they are in, you’d either have to create several maps (one from city name to population size and one from city name to state name) or you have to store a record instance as the value that holds both. The following code shows the option with the two maps:

  src

And here is the solution with the record:

  src

Note that some languages use the term dictionary for what we call a map.

Continue with Decisions and Calculations